Dynamic programming is the process of splitting a complex problem into simpler sub-problems, storing the values of each sub-problem and saving time by using these values to calculate the complex problem.
Dynamic Programming Explained Simple
Programming dynamically consists mainly out of saving results of simple tasks so that you do not have to calculate them again.
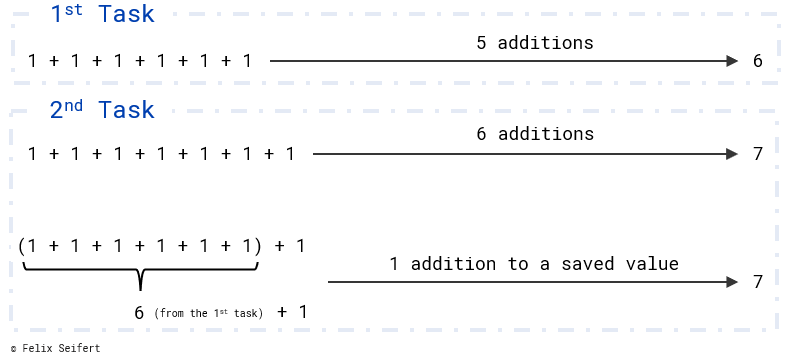
Assume a young kid who just learned addition in school. He/she writes down the task of calculating 1 + 1 + 1 + 1 + 1 + 1. After a short calculation, you know the solution is 6. Now, the kid adds a + 1 and asks you to calculate it. Of course, you could do the whole task of adding all the numbers again. But the idea of dynamic programming is using the previous result and adding the +1. Like this, you could get the solution quickly.
Use Case
Assume that you are living in a huge city and being the head of a bunch of high schools in this city. The students of one class completed an exam and you want to pair them up for studying together based on their results. The idea is to form groups of two with the results (in percentage) of both team mates adding up to 100%. You do not really want to start with forming pairs because there are so many possibilities. To simplify the process, you want to write an algorithm that calculates all the possibilities you have for selecting the first pair.
Basically, you want to know with how many different students each student could be paired up. As an input, you would receive a list with the results of all students.
Naive Approach
The naive idea would be looping through all the students in the list and for each student, looping the list again to find potential partners. In doing so, it is important to take into account that each student will not be matched to him/herself. (When one student has the result of 50%, two times itself is also 100%.)
public static long combineNaive(List<Integer> list) {
long result = 0;
for(int i = 0; i < list.size(); i++) {
for(int j = 0; j < list.size(); j++) {
if (list.get(i) + list.get(j) == 100 && i != j) {
result++;
}
}
}
return result/2;
}
At the end, the final result has to be divided by two because you do not want to double count (i.e. pairing up student A with student B and also student B with student A).
This solution results in looping ALL list entries for each list entry; for each of the n entries n calculations are performed. The time complexity of the algorithm is quadratic.
Improved Solution
The improved solution uses dynamic programming; it saves how often a certain result could be combined with the other results. If the list includes two students with the result of 20% and three students with 80%, each of the 20% students could be combined with the others three times.
Therefore, the algorithm saves how often certain kinds of students could be combined. Before the inner loop tries to combine the current student with all other students, it will be checked whether a student with the same result was already checked.
public static long combineImproved(List<Integer> list) {
long result = 0, temp;
// Map for storing already checked values
Map<Integer, Long> checked = new HashMap<>();
for(int i = 0; i < list.size(); i++) {
// Check whether the currently looped value was already checked
if(checked.containsKey(list.get(i))) {
result += checked.get(list.get(i));
}
// If the current value was not checked, compare it to all the other numbers
else {
temp = 0;
for(int j = 0; j < list.size(); j++) {
if(list.get(i) + list.get(j) == 100 && i != j) {
temp++;
}
}
result += temp;
checked.put(list.get(i), temp);
}
}
return result/2;
}
This algorithm is way faster and can be used for larger datasets. The algorithm complexity is quasilinear. In this manner, you could be in charge of even more schools with more students.
The two examples are implemented in Java and available on my GitHub page. Please do not hesitate to try the example and realise the difference for huge lists (lists could be generated automatically and processing times of the algorithms would be logged).