The MECE principle is a principle used to separate a set of items into different subsets. These subsets are both mutually exclusive and collectively exhaustive. In this article, I will explain what this means and how it can be useful for programming.
MECE stands for “mutually exclusive” (ME) and “collectively exhaustive” (CE). This principle originates from the huge management consultancy McKinsey & Company. The MECE principle can be used not only in the management sector but also in nearly every other sector where a clear and accurate separation is needed. Firstly, we will have a look at what the two parts of the MECE principle mean and how we can achieve them. Then, we will explore an example that shows how a set of items is accurately separated. Eventually, I will give some ideas how the MECE principle can be used in programming.
ME And CE
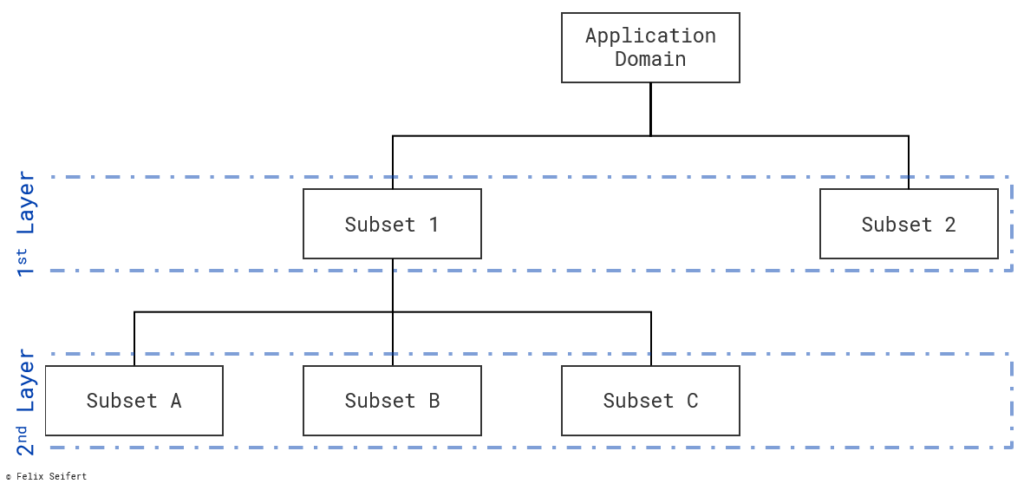
To start on the same grounds, figure 1 shows how the terms are used in a tree: A subset refines the application domain/ another subset and the total number of layers describes how often a refinement of the application domain took place.
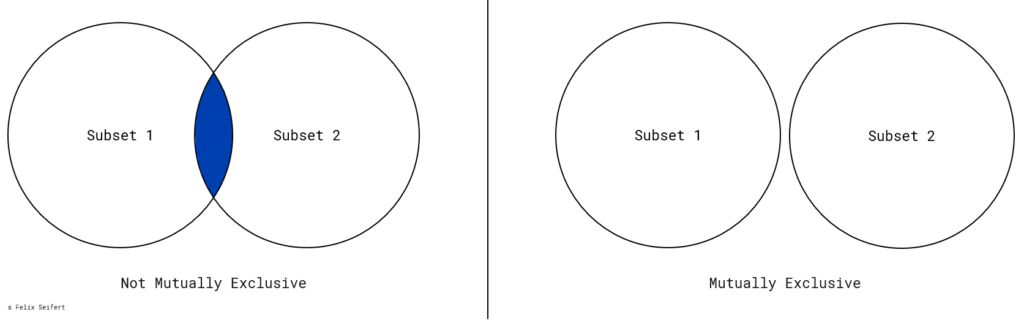
Mutually exclusive means that each item fits into only one subset of the same layer. It should never be unclear which subset to put an item into. Therefore, the definition of each subset does not overlap with and is exclusive from the definitions of the other subsets in this layer. The Venn diagrams in Figure 2 show the difference between non-exclusivity and exclusivity.
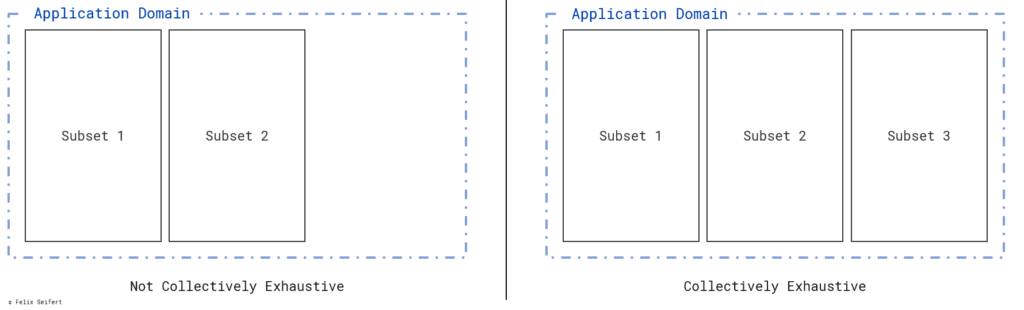
Collectively exhaustive means that a suitable subset can be found for every item on each layer. The subsets therefore have to exhaust all possible items of the application domain. The application domain describes the boundary in which the eventual sorting should be applied. So, we do not have to consider all the items which we can think of but only all the possible items in the application domain. Figure 3 visualises how the subsets collectively exhaust the application domain.
To summarise the separation rules of the MECE principle: Each item in the application domain fits in exactly one subset per layer.
Example
We want to build a new web shop for a customer. The customer runs a physical bike store and wants to sell its products online. A selection from the customer’s products include many mountain bikes, some city bikes and a few bicycles from random categories. The customer also sells back lights, front lights, locks, helmets and several small parts for repairing bicycles.
A Non-MECE Separation
The customer suggests a grouping which he/she created based on the products he/she sells. His/her subsets are as follows: mountain bikes, bicycles, helmets and locks and lights.
However, based on the previous principle, this separation represents a non-MECE separation. When a salesclerk wants to add a new mountain bike to the online store, he cannot be sure whether he should assign the new bike to the general subset bicycles or the more specific one mountain bikes. These two subsets are not mutually exclusive. The subset bicycles includes the whole subset mountain bikes. Another issue is that all the suggested subsets are not collectively exhaustive: even though small repair products might not be sold that often, the salesclerk is not able to assign them to a subset and therefore is unable to sell them in the web shop.
A MECE Separation
As we want to have a clear structure in the new online shop, we apply the MECE principle to figure out how the categorisation should be conducted. The easiest version which is MECE is to divide the web shop into the two subsets bicycles and non-bicycles. Just consider this as two parts which should add up to 1: x and 1-x, with x being somewhere from 0 to 1.
However, we want to have a more fine-grained separation such that the online shop becomes more usable. We achieve this by introducing multiple layers. One possible separation is to introduce the subsets bicycles and accessories on the first layer. On the second layer, we can separate the bicycles subset into mountain bikes, city bikes and other bikes. “Other…” is a very common way to ensure that all other products are covered; even when the portfolio of the shop might be expanded with some other bicycles in the future, the subsets do not necessarily have to be changed. For the other non-bicycle products in the subset accessories, we introduce the subsets lights, helmets, locks and other accessories (we again used the subset “other…” to ensure that we included all remaining products).
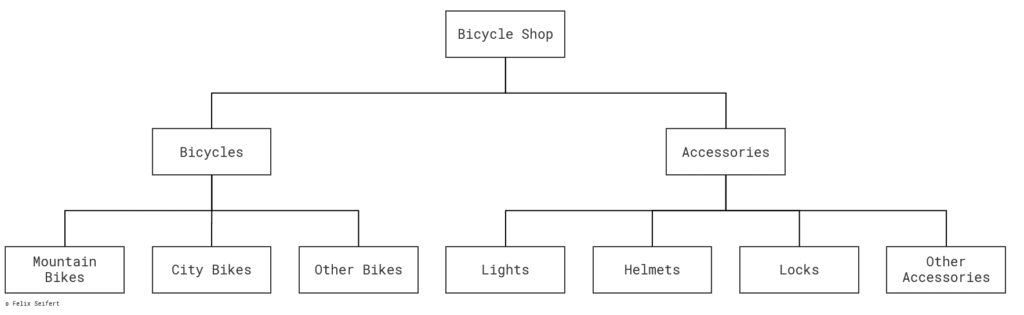
Figure 4 depicts the described separation. As we can now see, we do not find an issue of overlapping subsets anymore. Furthermore, the “other…” ensures that all products are included.
Extensibility of Separation
This is not the only way we can introduce a separation of the products of the bicycle shop. We can make it more fine-grained by deciding that since the shop sells so many helmets, the subset helmets can be separated in male helmets and female helmets on the next layer.
When the shop owner suddenly decides to sell touring bicycles, they definitely fit in the subset other bicycles. If the shop starts to sell bicycle jackets and trousers, the shop will need a new subset because they are neither bicycle accessories nor bicycles. Even though this would result in the creation of a new subset, this does not create too much trouble if the separation structure was properly considered at the start.
Conclusion
The MECE principle requires each item which should be categorised to fit into exactly one subset per layer. As an example, the previous section describes in-depth how the MECE principle can be applied. Based on different working styles, the task of the abovementioned example might be covered by the product or UX designers. However, software engineers can use the MECE principle in many other ways: e.g. dropdown list in forms, classes and their hierarchy/inheritance structure in object-oriented programming or the correct database design.